Nah Sobat , mau tau nggak sih bentuk umum persamaan kuadrat ? Gak cuma buat tugas sekolah aja lho , memahami persamaan kuadrat itu penting banget , apalagi buat kalian yang lagi belajar Matematika atau bahkan buat kalian yang hobinya ngitung-ngitung ! Persamaan kuadrat , ini nih ; sering banget muncul di berbagai bidang , mulai dari fisika , ekonomi , sampai desain grafis sekalipun ! Jadi , siap-siap , kita akan bahas tuntas bentuk umumnya , plus contoh-contoh yang bikin kalian langsung paham ,oke?

Bayangin aja , kalian lagi bikin desain jembatan , atau ngitung lintasan peluru ; persamaan kuadrat tuh kunci utamanya ! Karena , bentuknya yang unik , persamaan ini bisa ngegambarin berbagai fenomena alam & peristiwa sehari-hari , luar biasa kan ?. Nah , makanya , penting banget buat kalian ; ngerti betul-betul ; tentang bentuk umum persamaan kuadrat ini. Jangan sampe cuma asal ngerti aja lho ya ! .

Sebelum kita masuk ke inti pembahasan , ada baiknya , kita flashback sedikit mengenai apa itu persamaan kuadrat. Secara sederhana , persamaan kuadrat adalah persamaan polinom ; dengan pangkat tertinggi variabelnya adalah dua. Gimana , masih ingat pelajaran SMP ya ?. Bentuknya bisa macam-macam , tapi semua bisa disederhanakan ; ke dalam satu bentuk umum yang bakal kita bahas tuntas sekarang ini. Jadi , siapkan ; bolpoin & buku catatan kalian ya ! . Jangan sampai , kalian kelewatan poin-poin penting yang bakal kita bahas selanjutnya !

Bentuk umum persamaan kuadrat itu sendiri ; nyaman banget kok untuk diingat & dipahami. Rumusnya singkat , padat & jelas ; pasti kalian bakal langsung hafal , deh! Pokoknya , setelah baca artikel ini sampai selesai , kalian akan menjadi master ; persamaan kuadrat ! Dengan begitu , kalian gak perlu khawatir lagi ; ketika ketemu soal-soal ; yang berkaitan dengan persamaan kuadrat , bahkan soal olimpiade sekalipun ! Kalian udah siap untuk menjelajahi dunia persamaan kuadrat?. So , let’s go! Kita mulai dari memahami bentuk umum persamaan kuadrat ; & menjelajahi aplikasinya di berbagai bidang. Siap?

Bentuk‌ Umum‍ Persamaan Kuadrat: Panduan Lengkap‌ (20‍ Poin)

Pendahuluan: Mengenal‍ Persamaan Kuadrat dan‍ Pentingnya‍ Memahami Bentuk Umumnya!

Halo, Sobat‍ Matematika! Pernahkah‌ kamu‌ mendengar istilah‍ Persamaan Kuadrat? Persamaan‌ ini merupakan‌ salah‌ satu‌ konsep dasar‍ dalam aljabar yang‍ sangat penting untuk dipahami. Menguasai bentuk umumnya adalah kunci untuk‌ menyelesaikan berbagai masalah, baik‍ di dunia akademis‌ maupun‍ dunia‌ nyata. Artikel ini‌ akan memandu kamu‌ memahami bentuk umum Persamaan‌ Kuadrat‍ secara‍ detail, lengkap dengan‍ contoh dan penjelasan‍ yang mudah dicerna. Siap? Yuk, kita‍ mulai!

Memahami‌ Bentuk Umum Persamaan Kuadrat

Apa‌ Itu Persamaan Kuadrat?

Definisi‍ Persamaan Kuadrat‌ Sederhana.

Persamaan‌ kuadrat adalah‌ persamaan matematika‌ yang memuat variabel‍ berpangkat‍ dua (kuadrat) dan‌ tidak lebih‍ tinggi. Bentuk‍ paling‍ sederhana‍ ditandai dengan‍ adanya suku kuadrat, suku linear, dan‌ konstanta.

Contoh‌ Persamaan‍ Kuadrat‍ dalam Kehidupan‌ Sehari-hari‌ (Luas, Fisika, dll.)

Persamaan Kuadrat‌ bukan‍ hanya‍ teori‌ abstrak. Ia banyak diaplikasikan‌ dalam‌ kehidupan nyata! Misalnya, menghitung luas persegi panjang, menentukan lintasan gerak‌ parabola‍ dalam fisika, atau‍ memodelkan‍ pertumbuhan‌ populasi.

Perbedaan‌ Persamaan Kuadrat dengan‍ Persamaan Linear.

Perbedaan utama terletak‍ pada‍ pangkat tertinggi variabelnya. Persamaan‍ linear memiliki pangkat‌ tertinggi‌ satu, sedangkan‍ Persamaan Kuadrat‍ memiliki‌ pangkat‍ tertinggi dua. Grafiknya‍ pun‌ berbeda; persamaan‌ linear berupa garis lurus, sementara Persamaan Kuadrat‍ berupa‍ parabola.

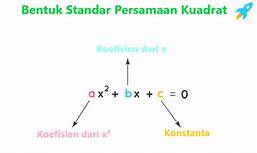
Bentuk‌ Umum‍ Persamaan Kuadrat: ax² + bx‍ + c‌ = 0

Penjelasan‌ Setiap‍ Variabel (a, b, c). Apa arti‌ dari setiap koefisien?

Bentuk umum Persamaan Kuadrat‌ ditulis‍ sebagai ax² + bx‌ + c = 0, di‌ mana:

• 'a' adalah‍ koefisien‍ dari‌ x², 'b' adalah‌ koefisien‌ dari x, dan‌ 'c' adalah‍ konstanta.

Syarat-syarat nilai a, b, dan‍ c‌ (a≠0). Mengapa a tidak boleh‍ nol? Apa yang‍ terjadi‍ jika‍ a=0?

Syarat‍ utama adalah a ≠ 0. Jika a‍ = 0, persamaan tersebut‍ bukan‍ lagi‌ Persamaan Kuadrat, melainkan‍ persamaan‌ linear!

Contoh Soal: Mengidentifikasi‍ nilai‍ a, b, dan c‍ dari berbagai‍ persamaan kuadrat.

Misalnya, pada‍ persamaan 2x² + 5x - 3 = 0, a = 2, b = 5, dan c = -3. Coba‌ kamu‍ identifikasi nilai‌ a, b, dan c pada persamaan‌ 3x² - 7x + 2 = 0‌ ?

Mengubah Bentuk Persamaan‌ Kuadrat‌ ke‍ Bentuk‍ Umum

Contoh Soal dan Langkah-langkah‍ Mengubah Persamaan‍ yang Bukan‌ Bentuk Umum.

Tidak‍ semua‌ Persamaan Kuadrat diberikan dalam‌ bentuk‍ umum. Kita‌ perlu‍ memanipulasi‌ aljabar‌ untuk‍ mengubahnya‍ ke‌ bentuk‍ ax² + bx + c = 0.

Menangani Persamaan‌ Kuadrat yang Memiliki‍ Bentuk Kompleks.

Persamaan yang kompleks‌ mungkin memerlukan‌ beberapa langkah manipulasi aljabar, seperti pengelompokan‍ suku, pemfaktoran, atau‌ penyederhanaan.

Tips dan‍ Trik untuk Mempermudah Proses Perubahan Bentuk Persamaan.

Selalu‍ pastikan untuk‌ menyederhanakan persamaan sebelum mengubahnya‌ ke bentuk umum. Perhatikan tanda positif‍ dan‌ negatif!

Menentukan‌ Jenis-jenis Persamaan‌ Kuadrat Berdasarkan Nilai Diskriminan‍ (D)

Rumus‌ Diskriminan (D = b² - 4ac) dan‌ Penjelasannya.

Diskriminan (D) menentukan jenis akar‌ dari‌ Persamaan‌ Kuadrat. Rumusnya adalah D‌ = b² - 4ac.

Mengenal‍ Jenis-jenis‍ Akar‍ Persamaan‌ Kuadrat‍ (Real‍ dan Imajiner, Tunggal dan Berbeda).

Nilai‍ D menentukan apakah‌ akarnya‌ real‌ atau‌ imajiner, dan apakah‍ akarnya tunggal atau‌ berbeda.

Contoh‌ Soal: Menentukan jenis‍ akar persamaan‍ kuadrat‌ berdasarkan‌ nilai diskriminan.

Misalnya, jika‍ D > 0, akarnya real‌ dan‌ berbeda. Jika D = 0, akarnya real‌ dan tunggal. Jika‍ D < 0, akarnya imajiner.

Aplikasi Persamaan Kuadrat dalam Berbagai Bidang‍

Penggunaan‌ Persamaan Kuadrat‍ dalam‌ Fisika (Gerak‌ Parabola, dll.)

Persamaan‍ Kuadrat sangat penting dalam‌ fisika, khususnya dalam‍ menggambarkan gerak parabola.

Aplikasi Persamaan Kuadrat‍ dalam‍ Ekonomi dan Bisnis.

Dalam ekonomi dan bisnis, Persamaan Kuadrat digunakan‌ untuk memodelkan‌ berbagai fenomena, seperti‌ permintaan dan‌ penawaran.

Persamaan‍ Kuadrat‌ dalam Perencanaan dan‌ Desain.

Persamaan Kuadrat‌ juga‍ berperan dalam‍ perencanaan dan desain, misalnya dalam‌ arsitektur‍ dan‍ teknik‍ sipil.

Metode-Metode Menyelesaikan‌ Persamaan Kuadrat‌ (Sekilas, link‌ ke‌ artikel lain yang‍ lebih detail)

Pemfaktoran.

Melengkapkan‍ Kuadrat‌ Sempurna.

Rumus Kuadratik.

Kesimpulan: Penguasaan‍ Bentuk‌ Umum Persamaan Kuadrat: Kunci Menuju Pemahaman yang Lebih‌ Dalam!

Memahami‌ bentuk umum Persamaan‍ Kuadrat adalah‍ langkah awal menuju pemahaman‌ yang lebih mendalam‍ tentang‌ konsep ini. Dengan latihan dan pemahaman‌ yang‌ baik, kamu‌ akan‍ mampu‌ menyelesaikan‌ berbagai permasalahan‌ yang‍ melibatkan Persamaan‌ Kuadrat.

FAQ‍ (Pertanyaan yang Sering Diajukan)

• Apa‌ yang dimaksud dengan‌ akar‌ persamaan‌ kuadrat? Akar‍ persamaan kuadrat‌ adalah‍ nilai x yang memenuhi persamaan‍ tersebut.
• Bagaimana‍ cara menggambar grafik‌ persamaan‌ kuadrat? Dengan‌ menentukan‍ titik‍ puncak‌ dan beberapa‌ titik‌ lainnya, lalu‌ menghubungkannya membentuk parabola.
• Apakah semua‍ persamaan kuadrat memiliki akar‍ real? Tidak, beberapa memiliki‌ akar imajiner.
• Apa aplikasi praktis‌ dari persamaan kuadrat di dunia‌ nyata? Banyak, mulai dari‌ fisika, ekonomi, hingga desain.

(Opsional) Tambahkan‍ beberapa latihan soal dan‌ kunci jawaban‍ di akhir artikel‌ untuk menguji‌ pemahaman pembaca.