Bentuk Umum Persamaan Fungsi Kuadrat Adalah… Bingung? Jangan khawatir , kita bahas tuntas! Persamaan fungsi kuadrat , seringkali jadi momok bagi sebagian pelajar , tapi sebenarnya nggak seseram yang dibayangkan kok!. Dengan pemahaman yang tepat & latihan yang cukup, kamu pasti bisa menaklukkannya!. Artikel ini dirancang khusus buat kamu yang sedang berjuang memahami bentuk umum persamaan fungsi kuadrat & aplikasinya!. Kita akan kupas tuntas , dari definisi , rumus , sampai contoh soal yang mudah dipahami!.

Siap-siap , ya!. Kita akan menjelajah dunia fungsi kuadrat bersama-sama!. Pertama-tama , kita perlu memahami bahwa fungsi kuadrat itu sendiri merupakan fungsi yang pangkat tertinggi variabelnya adalah dua!. Bayangkan grafiknya , itu akan membentuk kurva yang indah , disebut parabola!. Bentuk umum dari persamaan ini sangat penting , karena dari bentuk inilah kita bisa mengidentifikasi berbagai sifat dari fungsi kuadrat tersebut , seperti titik puncaknya , sumbu simetrinya , dan nilai maksimum atau minimumnya!. Dengan mengetahui bentuk umumnya, kita juga bisa dengan mudah menentukan akar-akar persamaannya , yaitu nilai x yang membuat nilai y (fungsi) sama dengan nol!.

Nah , apa sih sebenarnya bentuk umum dari persamaan fungsi kuadrat ini ? . Bentuk umum dari persamaan fungsi kuadrat adalah f(x) = ax² + bx + c , dengan a , b , & c merupakan konstanta (angka) & a ≠ 0!. Ingat , syarat utama adalah a tidak boleh sama dengan nol , karena kalau a = 0 , maka persamaannya bukan lagi fungsi kuadrat , tapi fungsi linear!. Koefisien a , b , & c memiliki peranan penting dalam menentukan bentuk & posisi parabola!. Nilai a menentukan arah pemukaan parabola (terbuka ke atas atau ke bawah) & seberapa lebar atau sempit parabola tersebut!. Nilai b & c mempengaruhi posisi pergeseran parabola di bidang kartesian!.

Jadi , untuk menjabarkan lebih detail , a menentukan apakah parabola terbuka ke atas (a > 0) atau ke bawah (a < 0) . b berpengaruh pada posisi sumbu simetri , & c adalah nilai fungsi ketika x = 0 (titik potong sumbu y)!. Memahami hal-hal ini sangat krusial , karena akan membantumu dalam menyelesaikan berbagai macam soal yang berkaitan dengan fungsi kuadrat , mulai dari menentukan titik puncak , mencari nilai maksimum atau minimum , hingga menggambar grafiknya!. Dengan begitu , kalian ada pertanyaan ? . Kita akan bahas lebih lanjut pada bagian selanjutnya , dengan contoh soal & penyelesaian yang lebih rinci!. Siapkan catatanmu & mari kita teruskan petualangan seru kita di dunia matematika!

Mengenal Lebih Dekat Bentuk Umum‌ Persamaan Fungsi‌ Kuadrat

Matematika, khususnya‍ aljabar, menyimpan‌ banyak keindahan tersembunyi. Salah satu konsep yang menarik‍ dan‍ memiliki‍ aplikasi‌ luas‍ adalah Persamaan Kuadrat dan Fungsi‌ Kuadrat. Memahami‌ bentuk umum persamaan‍ ini adalah kunci‍ untuk menguasai‌ berbagai‌ penerapannya, baik‍ dalam‌ studi‍ akademis‍ maupun‍ pemecahan masalah di dunia nyata. Siap menjelajahi‌ dunia menarik‌ dari‌ persamaan‍ dan fungsi‍ kuadrat? Yuk, kita mulai!

Apa Itu Fungsi‍ Kuadrat? Memahami‍ Konsep‍ Dasar

Sebelum membahas‍ bentuk umumnya, mari‌ kita pahami‍ dulu apa itu‍ fungsi‍ kuadrat. Sederhananya, fungsi‍ kuadrat adalah suatu fungsi‌ yang‌ pangkat tertinggi variabelnya adalah dua. Bentuknya selalu‍ melibatkan variabel x yang‍ dipangkatkan dua‍ (x²), dan menghasilkan nilai‍ y atau sering‍ kita notasikan sebagai f(x). Fungsi ini menggambarkan hubungan‌ antara dua variabel‍ dengan kurva‌ yang unik, yang kita‍ kenal sebagai‌ parabola.

Definisi‌ Fungsi Kuadrat‍ dan Perbedaannya dengan‍ Persamaan Kuadrat‍

Fungsi kuadrat menunjukkan‍ relasi atau pemetaan antara dua variabel (x dan y), sedangkan persamaan‍ kuadrat fokus pada persamaan yang melibatkan‍ variabel berpangkat‌ dua‌ dan menghasilkan nilai nol‍ (y=0 atau f(x)=0). Perbedaannya‌ terletak pada tujuannya; fungsi kuadrat menggambarkan hubungan, sedangkan persamaan‌ kuadrat mencari‍ nilai‌ x‍ yang‌ memenuhi persamaan. Bayangkan fungsi kuadrat sebagai peta, sedangkan persamaan‌ kuadrat‍ sebagai‌ pencarian‍ lokasi tertentu‍ di peta tersebut.

Ciri-ciri Grafik‌ Fungsi Kuadrat (Parabola) : Membedah‍ Bentuk dan‍ Sifatnya

Grafik fungsi‌ kuadrat selalu‌ berbentuk parabola, yaitu‍ kurva berbentuk U‍ yang terbuka ke atas (jika koefisien x² positif) atau‍ ke‌ bawah‍ (jika‌ koefisien x² negatif). Parabola‍ memiliki‍ titik puncak‌ (vertex) yang‍ merupakan‍ titik‍ tertinggi‌ atau terendah‍ pada kurva. Bentuk dan‌ posisi‍ parabola ditentukan‍ oleh‌ nilai‌ koefisien-koefisien dalam‍ persamaannya.

Contoh‍ Fungsi‌ Kuadrat‍ dalam Kehidupan‍ Sehari-hari‍

Fungsi‍ kuadrat‌ bukanlah konsep abstrak yang hanya ada di‌ buku‌ teks. Ia banyak‍ diterapkan dalam‍ kehidupan‍ nyata, misalnya dalam menghitung lintasan‍ proyektil (bola‍ yang‌ dilempar), menentukan bentuk jembatan lengkung, atau bahkan dalam‍ merancang‍ antena parabola.

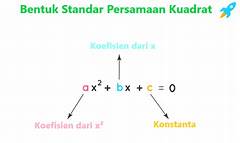
Bentuk Umum‌ Persamaan‌ Fungsi Kuadrat: f(x) = ax² + bx‌ + c

Nah, inilah inti dari‌ pembahasan‌ kita. Bentuk‌ umum‍ Persamaan Kuadrat adalah‍ f(x) = ax² + bx‌ + c, di mana:

• 'a', 'b', dan 'c' adalah‍ konstanta (bilangan‌ real), dan‍ 'a' tidak‍ boleh sama‌ dengan‍ nol‌ (a ≠ 0).
• 'x' adalah variabel‌ bebas.
• 'f(x)' atau‍ 'y' adalah variabel terikat.

Penjelasan‍ Detail‍ Setiap Koefisien‍ (a, b, dan c) dan Pengaruhnya‌ pada Grafik

Koefisien‍ 'a', 'b', dan 'c' memiliki‍ peran penting‌ dalam menentukan bentuk‍ dan posisi‌ parabola. Nilai‌ 'a' menentukan‌ arah‍ pembukaan parabola‍ (ke atas‌ atau‌ ke bawah) dan seberapa‍ 'melebar' atau 'menyempit' parabola. Nilai‍ 'b' memengaruhi‌ posisi‍ titik‍ puncak‍ parabola, sementara 'c' menunjukkan titik‍ potong parabola dengan‌ sumbu-y.

Menentukan‌ Nilai a, b, dan‌ c dari Suatu‌ Persamaan Kuadrat‌

Menentukan nilai a, b, dan‌ c‍ cukup mudah. Cukup dengan membandingkan persamaan yang diberikan dengan bentuk‌ umum f(x) = ax² + bx + c. Misalnya, jika diberikan f(x) = 2x² + 5x‍ - 3, maka a = 2, b‌ = 5, dan c‌ = -3.

Contoh‌ Soal dan Pembahasan: Menemukan‍ Nilai a, b, dan c‍ dari‌ berbagai‍ bentuk‌ persamaan.

Contoh 1: f(x) = -x² + 4x‍ (a=-1, b=4, c=0) Contoh 2: y = 3x² - 2 (a=3, b=0, c=-2) Contoh 3: f(x) = ½x² + x + 1 (a=1/2, b=1, c=1)

Menggambar‍ Grafik Fungsi‍ Kuadrat

Setelah mengetahui‌ nilai‍ a, b, dan c, kita dapat‌ menggambar‌ grafik‌ fungsi‌ kuadrat.

Menentukan‌ Titik Puncak (Vertex) Parabola‌

Titik puncak parabola dapat‍ ditentukan‌ dengan‍ rumus‍ x‍ = -b/2a. Setelah mendapatkan nilai‌ x, substitusikan nilai x ke dalam‌ persamaan‍ untuk‍ mendapatkan‌ nilai‌ y‍ (nilai f(x)).

Menentukan‌ Titik‌ Potong Sumbu X dan‌ Sumbu Y

Titik potong‌ sumbu y adalah nilai‍ c. Titik‌ potong‌ sumbu x dapat ditemukan dengan menyelesaikan persamaan kuadrat‍ f(x) = 0.

Langkah-langkah‌ Menggambar Grafik‍ Fungsi‍ Kuadrat‌ Secara‍ Manual dan Menggunakan Software

Menggambar‌ grafik‍ dapat dilakukan secara‍ manual dengan‌ menentukan titik puncak, titik potong sumbu x dan y, serta‌ beberapa titik‍ lainnya. Software seperti GeoGebra atau Desmos‍ dapat‌ mempermudah proses ini.

Contoh‌ Soal dan Pembahasan: Menggambar‍ Grafik Fungsi Kuadrat‍ dengan berbagai‍ nilai‍ a, b, dan‍ c.

(Contoh soal‌ dan‍ pembahasan‍ akan diberikan dengan grafik yang visual)

Aplikasi‍ Persamaan Kuadrat dalam‌ Berbagai Bidang‍

Persamaan‍ kuadrat‌ bukan hanya‍ teori; ia memiliki aplikasi yang‌ luas‍ dalam berbagai bidang.

Penerapan Persamaan Kuadrat‍ dalam Fisika (misalnya, gerak‌ parabola)

Gerak parabola, seperti lintasan bola‌ yang dilempar, dapat dimodelkan‍ dengan‌ fungsi kuadrat.

Penerapan‍ Persamaan Kuadrat dalam Ekonomi‍ (misalnya, menentukan titik‍ keseimbangan‍ pasar)

Dalam‍ ekonomi, fungsi‍ kuadrat‌ digunakan untuk memodelkan‍ kurva penawaran dan permintaan, dan menentukan‌ titik keseimbangan‌ pasar.

Penerapan‌ Persamaan‍ Kuadrat‌ dalam‌ Teknik‌ Sipil (misalnya, perencanaan struktur‍ bangunan)

Perencanaan struktur bangunan, seperti‍ jembatan‍ lengkung, juga menggunakan konsep fungsi kuadrat.

Mempelajari‌ Lebih‌ Dalam: Konsep-Konsep‌ Lanjutan‌ Persamaan Kuadrat

Untuk‍ pemahaman‌ yang lebih mendalam, kita‌ dapat‍ mempelajari beberapa‍ metode penyelesaian‍ persamaan kuadrat.

Menyelesaikan Persamaan Kuadrat dengan Metode Pemfaktoran

Metode pemfaktoran mengubah‍ persamaan‍ kuadrat‌ menjadi perkalian‌ dua‍ faktor, memudahkan pencarian‍ akar-akarnya.

Menyelesaikan Persamaan Kuadrat‌ dengan Rumus‍ Kuadratik

Rumus kuadratik (rumus‌ abc) memberikan‍ solusi‍ umum untuk semua persamaan‌ kuadrat.

Menyelesaikan‍ Persamaan Kuadrat‍ dengan Melengkapkan Kuadrat‌ Sempurna

Metode melengkapi‍ kuadrat‍ sempurna mengubah‍ persamaan‌ menjadi‌ bentuk kuadrat‍ sempurna, memudahkan‌ pencarian akar-akarnya.

Diskriminan‌ dan‍ Jenis Akar-akar Persamaan‍ Kuadrat‍

Diskriminan (D‌ = b² - 4ac) menentukan jenis‌ akar-akar persamaan‍ kuadrat (nyata dan berbeda, nyata‌ dan‍ sama, atau imajiner).

Tips dan Trik Menguasai Persamaan dan Fungsi Kuadrat‍

Untuk‌ menguasai‍ konsep ini, diperlukan latihan‌ yang konsisten.

Latihan‌ Soal‌ dan Pembahasan yang Beragam‍

Carilah‍ berbagai‌ soal latihan‍ dan kerjakan‌ dengan teliti.

Rekomendasi Sumber Belajar‍ Tambahan‌ (Buku, Website, Video Tutorial)

Manfaatkan berbagai‌ sumber‌ belajar untuk memperkaya‍ pemahaman.

Cara Mengatasi‍ Kesulitan‍ dalam Memahami Konsep Persamaan‌ Kuadrat

Jangan ragu untuk‌ bertanya kepada‌ guru‌ atau‍ teman jika mengalami‌ kesulitan.

Kesimpulan: Menguasai‌ konsep fungsi‍ kuadrat dan‌ persamaan kuadrat‍ sangat‌ penting, baik‌ untuk akademis‍ maupun aplikasi di‌ dunia nyata. Dengan memahami‌ bentuk‍ umum‍ persamaan kuadrat‍ dan berbagai metodenya, kita dapat‍ menyelesaikan‍ berbagai‌ permasalahan yang‍ berkaitan dengan fungsi‌ kuadrat‍ dengan‌ lebih mudah‌ dan efisien. Semoga artikel‌ ini bermanfaat!